ÍNDICE
Contenidos
![]()
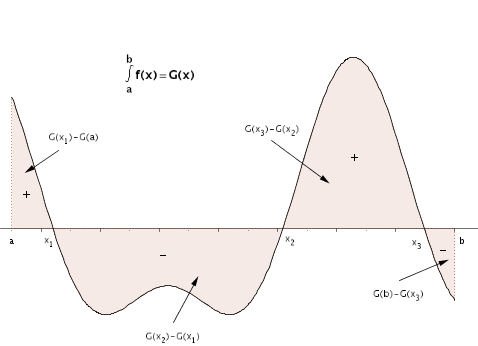
En ese caso, por otro lado común, el valor de la integral no representa el valor del área que queremos calcular, pues las partes negativas se restarán de las positivas, llevándonos a error.
Por tanto, lo que vamos a hacer en estos casos es encontrar los trozos y sumar el valor del área de cada trozo transformado en positivo.
En resumen, para hallar el área que estamos buscando sería bueno seguir los siguientes pasos:
1.- Resolver la ecuación $f(x)=0$ para averiguar los puntos de corte de la curva con el eje $X$.
2.- Seleccionar las raices que se encuentran entre $a$ y $b$. Supongamos que estas raíces, ordenadas de menor a mayor, son:
$$a \lt x_1 \lt x_2 \lt x_3 \lt b$$
3.- Buscar una primitiva de $f(x)$. Llamémosla $G(x)$.
4.- Calcular $G(a), G(x_1), G(x_2), G(x_3) $ y $G(b)$.
5.- Según la regla de Barrow, $G(x_1)-G(a), \, G(x_2)- G(x_1), \, G(x_3)-G(x_2), \, G(b)- G(x_3)$
son las integrales de los cuatro recintos en los que está
dividida el área buscada. Si tomamos sus valores absolutos y
sumamos los cuatro valores tendremos el valor del área.
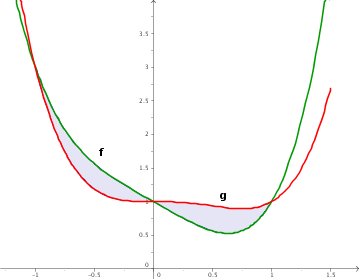
Área comprendida entre dos curvas
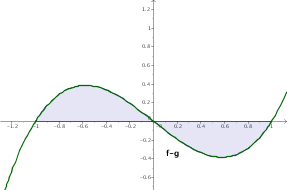
El área comprendida entre dos curvas, $f$ y $g$, es la misma que la comprendida entre la función $f-g$, y el eje $OX$, como vemos en la figura.