ÍNDICE
Contenidos
![]()
LA FUNCIÓN ÁREA
Dada una función $f$, continua en $[a,b]$, podemos calcular $\displaystyle\int_a^c f$ para todo número $c \in [a,b]$.
Consideremos la nueva función $F(x)=\displaystyle\int_a^x f, \, x\in [a,b]$, que no es otra cosa que el área que hay bajo $f$ entre a y un punto variable x del intervalo.
Es evidente que cuanto mayor sea la ordenada de $f$, más rapidamente crece el área bajo ella y por tanto mayor es $F'$. También es obvio, que cuando $f$ es negativa, lo es su área, por tanto $F$ decrece y su derivada es negativa. En el próximo teorema vamos a ver al relación entre $F'$ y $f$.
TEOREMA FUNDAMENTAL DEL CÁLCULO
Si $f$ es una función continua en $[a,b]$, entonces la función $F(x)=\displaystyle\int_a^x f$, es derivable, y se verifica que $F'(x)=f(x)$.
Demostración:
Vamos a calcular $F'(x)$, para lo cual vamos a calcular $$\lim\limits_{h \rightarrow 0}\frac{F(x+h)-F(x)}{h}$$
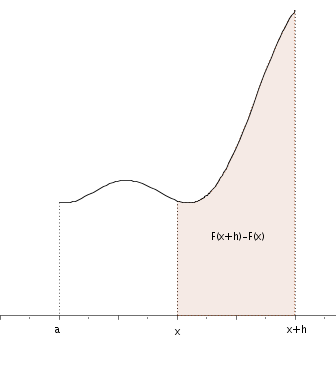
De esa forma llegamos a aquello que queríamos demostrar: $F'(x)=f(x)$.